publications

2023

1. 

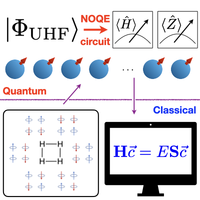   Say NO to Optimization: A Nonorthogonal Quantum Eigensolver

   Unpil Baek, Diptarka Hait, James Shee, and 5 more authors

   PRX Quantum, Jul 2023

   Abs DOI

   A balanced description of both static and dynamic correlations in electronic systems with nearly degenerate low-lying states presents a challenge for multiconfigurational methods on classical computers. We present here a quantum algorithm utilizing the action of correlating cluster operators to provide high-quality wave-function ansätze employing a nonorthogonal multireference basis that captures a significant portion of the exact wave function in a highly compact manner and that allows computation of the resulting energies and wave functions at polynomial cost with a quantum computer. This enables a significant improvement over the corresponding classical nonorthogonal solver, which incurs an exponential cost when evaluating off-diagonal matrix elements between the ansatz states and is therefore intractable. We implement the nonorthogonal quantum eigensolver (NOQE) here with an efficient ansatz parametrization inspired by classical quantum chemistry methods that succeed in capturing significant amounts of electronic correlation accurately. Crucially, we avoid the need to perform any optimization of the ansatz on the quantum device. By taking advantage of such classical approaches, NOQE provides a flexible, compact, and rigorous description of both static and dynamic electronic correlation, making it an attractive method for the calculation of electronic states of a wide range of molecular systems.

2020

1. A non-orthogonal variational quantum eigensolver

   William J Huggins, Joonho Lee, Unpil Baek, and 2 more authors

   New Journal of Physics, Jul 2020

   Abs DOI

   Variational algorithms for strongly correlated chemical and materials systems are one of the most promising applications of near-term quantum computers. We present an extension to the variational quantum eigensolver that approximates the ground state of a system by solving a generalized eigenvalue problem in a subspace spanned by a collection of parametrized quantum states. This allows for the systematic improvement of a logical wavefunction ansatz without a significant increase in circuit complexity. To minimize the circuit complexity of this approach, we propose a strategy for efficiently measuring the Hamiltonian and overlap matrix elements between states parametrized by circuits that commute with the total particle number operator. This strategy doubles the size of the state preparation circuits but not their depth, while adding a small number of additional two-qubit gates relative to standard variational quantum eigensolver. We also propose a classical Monte Carlo scheme to estimate the uncertainty in the ground state energy caused by a finite number of measurements of the matrix elements. We explain how this Monte Carlo procedure can be extended to adaptively schedule the required measurements, reducing the number of circuit executions necessary for a given accuracy. We apply these ideas to two model strongly correlated systems, a square configuration of H4 and the π-system of hexatriene (C6H8).